
Der Lunar Reconnaissance Orbiter (LRO) der NASA hat die schärfsten Bilder der Landeplätze von Apollo 12, 14 und 17 aufgenommen, die jemals vom Weltraum aus gemacht wurden. Die Aufnahmen zeigen die Wendungen der Pfade, die von den Astronauten hinterlassen wurden, als sie die Mondoberfläche untersuchten.
Am Landeplatz von Apollo 17 sind die von dem Mondrover gemachten Spuren deutlich sichtbar, zusammen mit den letzten Fußabdrücken auf dem Mond. Die Bilder zeigen auch, wo die Astronauten einige der wissenschaftlichen Instrumente abstellten, die den ersten Einblick in die lunare Umgebung und das Innere des Mondes lieferten.
„Wir können die Schritte der Astronauten mit größerer Genauigkeit zurückverfolgen, um zu sehen, wo sie die Proben genommen haben“, sagte Noah Petro, ein Mondgeologe vom Goddard Space Flight Center der NASA in Greenbelt (Maryland) und Mitglied des LRO-Wissenschaftsteams.

Oben/unten: Diese zwei LRO-Bilder zeigen die Landestelle von Apollo 17. Das obere Bild wurde gestern veröffentlicht, das untere ist eine gezoomte Aufnahme aus dem Jahr 2009. Aufgrund von unterschiedlichen Lichtbedingungen, einem anderen Kamerawinkel und diverser anderer Parameter stimmen die Bilder nicht perfekt überein. Helligkeit und Kontrast wurden optimiert, um Oberflächendetails hervorzuheben.
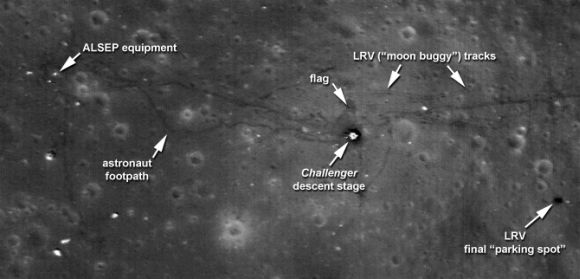
Alle drei Bilder zeigen klare Abdrücke in der dünnen Bodenschicht, als die Astronauten die Mondfähren verließen und den Mond zu Fuß erkundeten. Auf dem Bild von Apollo 17 sind die Fußabdrücke – darunter die letzte von Menschen hinterlassene Spur auf dem Mond – leicht von den doppelten Spuren des Mondrovers zu unterscheiden, welcher östlich der Landefähre parkt.
„Die neue Narrow Angle Camera schärft unseren Blick auf die Mondoberfläche aus geringer Höhe“, sagte Mark Robinson von der Arizona State University und leitender Wissenschaftler für die Lunar Reconnaissance Orbiter Camera (LROC). „Ein gutes Beispiel ist die Schärfe der Rover-Spuren am Landeplatz von Apollo 17. Auf vorherigen Bildern waren die Spuren zwar sichtbar, aber jetzt sind es scharfe, parallele Linien auf der Oberfläche.“

Oben/unten: Diese zwei LRO-Bilder zeigen die Landestelle von Apollo 12. Das obere Bild wurde gestern veröffentlicht, das untere ist eine gezoomte Aufnahme aus dem Jahr 2009. Aufgrund von unterschiedlichen Lichtbedingungen, einem anderen Kamerawinkel und diverser anderer Parameter stimmen die Bilder nicht perfekt überein. Helligkeit und Kontrast wurden optimiert, um Oberflächendetails hervorzuheben.
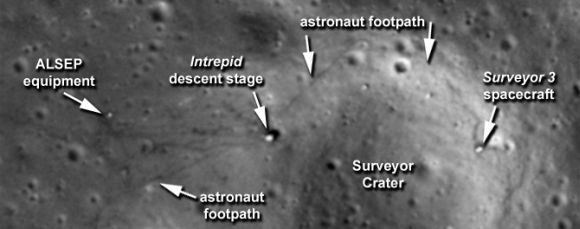
An jedem Landeplatz führen die Abdrücke auch nach Westen, wo die Astronauten das Apollo Lunar Surface Experiments Package (ALSEP) platzierten, um die Umgebung und das Innere des Mondes zu aufzuzeichnen.
Dieses Equipment war ein entscheidender Teil jeder Apollo-Mission. Es lieferte die ersten Einblicke in die innere Struktur des Mondes, Messungen des Oberflächendrucks und der Zusammensetzung seiner Atmosphäre. Apollo 11 hatte eine einfachere Version dieser wissenschaftlichen Ausrüstung an Bord.
Eine der auffälligen Einzelheiten ist eine helle L-Form auf dem Bild von Apollo 12. Es markiert die Positionen von Kabeln, die von der Zentralstation des ALSEP zu zwei seiner Instrumente verlaufen. Obwohl die Kabel viel zu klein sind, um direkt gesehen zu werden, fallen sie auf, weil sie das Licht sehr gut reflektieren.
Video-Link: https://youtu.be/_WZ26s4ik2w
Die höhere Auflösung dieser Bilder ist möglich, weil an der leicht ovalen oder elliptischen Umlaufbahn des LRO Änderungen vorgenommen wurden. „Ohne die durchschnittliche Höhe zu verändern, machten wir die Umlaufbahn elliptischer, so dass der niedrigste Teil des Orbits auf der sonnenbeleuchteten Seite des Mondes ist“, sagte John Keller, LRO Projektwissenschaftler am Goddard Space Flight Center. „Das brachte den LRO in die perfekte Position, um diese neuen Aufnahmen der Mondoberfläche zu machen.“
Das Manöver senkte den LRO von seiner normalen Höhe von annähernd 50 Kilometern auf eine Höhe von knapp 21 Kilometern ab, als er die Mondoberfläche überflog. Die Sonde blieb 28 Tage lang in dieser Umlaufbahn, lange genug für eine vollständige Umdrehung des Mondes. Das erlaubt die komplette Abdeckung der Oberfläche durch die Wide Angle Camera der LROC. Der Zyklus endete am 6. September 2011, als die Sonde zurück in ihren 50-Kilometer-Orbit gebracht wurde.

„Diese Bilder erinnern uns an die fantastische Apollo-Geschichte und geben uns ein Zeichen, die Erforschung unseres Sonnensystems voranzutreiben“, sagte Jim Green, Direktor der Planetary Science Division am NASA-Hauptquartier in Washington.
Der LRO wurde vom Goddard Space Flight Center gebaut und wird von selbigem betrieben. Die grundlegende Forschung wurde vom Exploration Systems Mission Directorate am NASA-Hauptquartier finanziell unterstützt. Im September 2010, nach einer einjährigen Erkundungsmission, richtete die Misson ihr Augenmerk weg von Beobachtungszielen hin zu wissenschaftlicher Forschung am NASA Science Mission Directorate.
Quelle: http://www.nasa.gov/mission_pages/LRO/news/apollo-sites.html
(THK)
SIEGFRID MARQUARDT: „Die Astronauten von Apollo 11 bis N haben ganz lustig acht und mehr Tage lang die Erde umrundet.“
Wieso UMRUNDET? Die Erde ist doch flach! :-p
Es ist sehr traurig, dass manche Menschen mit Zahlen und mathematischen Symbolen versuchen die Leute, die sich damit nicht auskennen, zu impressionieren. Hier werden grundlegende physikallische Gesetze einfach ignoriert! Dabei vergessen solche möchtegern-Wissenschaftler, dass astropage.eu auch von professionellen Astrophysikern gelesen wird, die auf diese dilettantischen Ausführungen nur mit einem Rat reagieren können: Befassen Sie sich bitte, zumindest mit der Physik für Anfänger, bevor Sie sich als ungebildet auf diesem Sektor vor der Öffentlichkeit blamieren! Ich habe mindestens 3 Stellenn im Internet gefunden, von wo diese „Berechnungen“ blind abgeschrieben wurden. Eine Stelle davon erklärt sogar die Echtheit der Mondlandung. Also, Herr Marquard, diese Texte hier waren ein schweres Eigentor, ich freue mich, dass solchem blödsinnigen Treiben hier ein Riegel vorgeschoben wird.
Widerlegung des Andockmanövers/Wendemanövers von CSM an die Mondlandefähre über eine Energiebetrachtung
Im Internet ist hierzu folgendes zu lesen: Apollo 11 startete am 16. Juli 1969 um 13:32:00 UTC an der Spitze der 2940 Tonnen schweren Saturn V von Cape Canaveral, Florida und erreichte zwölf Minuten später planmäßig die Erdumlaufbahn. Nach anderthalb Erdumkreisungen wurde die dritte Raketenstufe erneut gezündet. Sie brannte etwa sechs Minuten lang und brachte das Apollo-Raumschiff auf Mondkurs. Kurze Zeit später (!!! Also faktisch nach 6 Minuten) wurde das Kommando/Servicemodul (CSM) an die Landefähre angekoppelt (laut Wikipedia, Fassung vom 29.12.2017). Damit müsste sich das CSM Columbia nach 6 Minuten ca. 4000 km von der Erde entfernt gehabt haben (v*t=11 km/s*6*60 s=3960 km ≈ 4000 km). In einer Entfernung von ca. 4000 km von der Erde beträgt die Erdbeschleunigung nur noch
g40000 km= (6375 km: 10375 km)²*9,81≈ 3,7 m/s². (1)
Damit wäre bei einer Masse des CSM von 30.000 kg und einer Höhe (Länge) von 11 m (siehe Wikipedia vom 29.12.2017) eine Energie von
E180o=m*g*H*π*0,5= 30.000 kg*3,7 m/s²*11*3,14*0,5 Nm ≈1,9 MJ ≈ 2 MJ (2)
erforderlich gewesen, um das Raumschiff CSM zum Andocken an die Mondlandefähre um 180o zu drehen. Für das Wendemanöver standen aber lediglich 16 Düsen à 441 N zur Verfügung. Die Gesamtenergie, die die Düsen maximal für das Wendemanöver hätten liefern können, hätte lediglich
ED= S*H*0,5 = 16*441 N*11 *0,5 m ≈ 38 kJ≈40 kJ. (3)
Betragen können. Damit hätte die Energie der Steuerdüsen bei weitem nicht für das Andockmanöver ausreichen können!
Siegfried Marquardt, Königs Wusterhausen
Wie alle bisherigen Kommentare dieses in Fachkreisen bekannten und berüchtigten Verschwörungstheoretikers wurde auch dieser Kommentar als abschreckendes Beispiel freigegeben. Die Leser, die sich intensiver mit diesen Themen beschäftigen, wissen natürlich, dass seine Ausführungen weit in Bereich der Verschwörungstheorien fallen und keinerlei wissenschaftliche Grundlage haben. Die Leser, die sich noch nicht tiefgehender mit den physikalischen Grundlagen bezüglich Mondlandung und Raketentechnik beschäftigt haben, brauchen seine Ausführungen nicht ernst nehmen – sie sind Blödsinn, salopp gesagt.
Da das Fazit „Mondlandungsfake = Blödsinn“ bekannt ist oder bekannt sein sollte, werden seine Kommentare ab jetzt als pseudowissenschaftlicher Spam betrachtet und nicht mehr freigegeben bzw. gelöscht.
Bei den vermeintlichen Aufnahmen von Apollo 12; 14 und 17 handelt es sich eindeutig um Manipulationen! Denn aus 100 km Höhe ergibt sich bei einer Dimensionierung eines Objektes von ca. 4 m ein Sehwinkel von 4*10hoch-5. Diese Objekte, wie Apollo 12; 14 und 17 könnten damit niemals wahrgenommen werden! Die Gründe das Apollo 11 bis 17 niemals stattgefunden haben sind folgende:
Mathematisch-physikalische Widerlegung von Apollo 11 bis N
1. Aufgrund der Parameter der Saturnrakete konnte Apollo 11 niemals das Schwerefeld der Erde verlassen, um mit der 2. Kosmischen Geschwindigkeit von 11,2 km/s zum Mond zu gelangen. Dies lässt folgende Tabelle 1 und nachfolgende Berechnungen erkennen:
Tabelle 1: Treibstoffkombinationen der einzelnen Stufen mit den Start- und Leermassen und den effektiven Ausströmgeschwindigkeiten ve der Raketentreibstoffe (Leitenberg, B, 2013 und NASA im Internet 2014).
Stufe N/Treibstoff Mo t ML t ve m/s Bemerkungen
1. RP (Kerosin) + O2 2286 135 2600
2. H2 + O2 490 39 4200/3600 ve ist anzuzweifeln – 3570 sind realistisch; denn es gilt ve= 0,7 *vmax= 5100 m/s *0,7= 3570 m/s
3. H2 + O2
+ CSM +LM 119 +
45 13 +
45 4200/3600 Dto. – 3570 sind realistisch
∑ 2945
Entsprechend der Raketengrundgleichung
vB= ve * ln (MO: Ml) (1)
könnte man mit den drei Stufen nach einer Modifikation der Formel (1) theoretisch eine maximale Bahn- und Brennschlussgeschwindigkeit von
vB= 2,6 km/s*ln (2940:654) + 3,6 km/s* [ln(654:164) + ln (164:58)] ≈ 2,6 km/s*1,5 +
3,6*km/s (1,4 +1) = 3,9 km/s+ 3,6 km/s*2,4 = 3,9 km/s+ 8,6 km/s = 12,5 km/s (2)
ohne Berücksichtigung der Gravitation und des Luftwiderstandes erzielen. Für die Gravitation müssen für das Erreichen des Erdorbits in 200 km Höhe mindestens ein Betrag von
∆ v= √2*200.000 m *9,5 m/s² = 2000 km/s= 2 km/s (3)
von den 12,5 km/s abgezogen werden. Und für den Luftwiderstand 0,6 km/s. Dies ergibt Summa Summarum 9,9 km/s. Dieser Betrag liegt signifikant unter dem Wert der Fluchtgeschwindigkeit von 11,2 km/s! Damit konnte Apollo 11 gerade einmal komfortabel den Erdorbit erreichen. Es kommt aber noch schlimmer für Apollo 11: nach Wolff (1966) konnten in den sechziger Jahren höchstens ve von 2600 m/s erzielt werden. Damit konnte Apllo11 mit den deklarierten Parametern der NASA aber damals allerdings nur eine Brennschlussgeschwindigkeit von
vB= 3,9 km/s+ (2,6* 2,4 km/s) = (3,9 + 6,24) km/s = 10,14 km/s
erzielen. Zieht man davon die 2,6 km/s ab, die auf die Gravitation und den Luftwiderstand beruhen, dann ergibt sich eine maximale Bahngeschwindigkeit von gerade einmal
vB= (10,44 – 2,6) = 7,84 km/s. Damit konnte Apollo 11 gerade einmal ganz knapp die Erdumlaufbahn erreichen!
2. Nach Sternfeld (1959) sollen nur zwei ca. 14-Tageskonstellationen und ein 60-Tageszenario existieren, um den Mond mit einem künstlichen Raumflugkörper von der Erde aus zu erreichen und auf der Erde wieder zu landen. Unabhängig von den theoretischen Fakten und Details von Sternfeld, benötigte der Forschungssatellit SMART I, der Ende September 2003 gestartet wurde, 49 Tage bis auf die Mondebene und fünf Monate bis die Sonde in die Mondumlaufbahn einmündete. Und die im Dezember 2013 erfolgreich verlaufende Mondexpedition der chinesischen Sonde Chang`e-3 bewies bestechend, dass man mindestens 14 Tage zur Bewältigung der Distanz von der Erde zum Mond benötigt. Damit wäre Apollo 11 bereits eindrucksvoll empirisch widerlegt, weil ein vermeintliches 8-Tagesregime, das angeblich mit Apollo 11 praktiziert und exerziert wurde, astrophysikalisch theoretisch und empirisch überhaupt nicht existiert!
3. Die kosmische Strahlung, die auf die Astronauten innerhalb der 8 Tage eingewirkt hätte, wäre absolut infaust gewesen! Denn: Sie hätten je nach gewählter Modellrechnung eine tödliche Strahlendosis von mindestens 11 Sv bis 26 Sv inkorporiert. wenn man in diesem Zusammenhang an die hochenergetische Teilchendichte im Kosmos und an den Partikelstrom der Sonne mit der Solarkonstante von 8,5*1015 MeV/m²*s denkt. Nach Lindner (1973) treffen pro Sekunde auf einen Quadratmeter 1300 Protonen aus dem Kosmos auf die Erdatmosphäre ein. Rechnet man diese Energie auf die 8 Tage währende „Mondmission“ hoch, dann ergäbe sich die gewaltige Strahlendosis von weit über 1000 Sv! Die Astronauten hätten den Flug zum Mond und zur Erde zurück in jedem Falle nicht überlebt, da die absolut tödliche Dosis bei 10 Sv liegt. Damit wäre Apollo 11 und N absolut widerlegt!
4. Es fehlten insgesamt über 80 t Raketentreibstoff, um von der Erde zum Mond und von dort wieder zurück zur Erde auf der von der NASA vorgegebenen schleifenförmigen Flugbahn zu gelangen. Dies ergibt folgende Bilanz:
Für den Einschuss ins All mit 11,2 km/s wären für die 45 t Masse des Kommandoservicemoduls CSM und Lunamodul eine Treibstoffmenge von
MTr=[1-(1: e(vB/ve))]*Mo= [1-(1:2,72 (3,3:3,6))]*45 t = (1- 0,4)* Mo≈ 0,6*45 t≈ 27 t (4)
Erforderlich gewesen. Das Kommandoservicemodul CSM mit dem Mondlandemodul hätte mit einer Geschwindigkeit von 2,4 km/s in die Sphäre des Mondes gelangen müssen. Für das Abbremsen der zweiten kosmischen Geschwindigkeit von 2,4 km/s des Mondes auf die Orbitgeschwindigkeit von 1,6 km/s (∆vB=2,4 km/s-1,7 km/s= 0,7 km/s), wäre eine Treibstoffmasse bei einer effektiven Ausströmgeschwindigkeit von 2,6 km/s von
MTr= [1 – 1: e(vB/ve)]*Mo= [1-1: 2,72 (0,7:2,6)]* 45 t = (1- 0,76)* 45 t≈ 0,24*45 t≈ 11 t (5)
einzukalkulieren. Für die Landung aus einem 100 km-Orbit (+ ca. 0,56 km/s sind für die Wirkung der Schwerkraft des Mondes zusätzlich einzukalkulieren) auf dem Mond wäre bei 15 t der Startmasse Mo des Mondlandemoduls und ∆vB=2,3 km/s eine Treibstoffmasse bei einer effektiven Ausströmgeschwindigkeit von 2,6 km/s von
MTr=[1 – 1: e(vB/ve)]*Mo= [1-1: 2,72 (2,3:2,6)]*15 t) = (1- 0,41)*15 t ≈
0,59*15 t ≈ 9 t (6)
zu beziffern. Für den Start vom Mond mit der Aufstiegsstufe mit einer Startmasse von 4,7 t benötigt man
MTr= [1 – 1: e(vB/ve)]*Mo= [1-1: 2,72 (2,3:2,6)]*4,7 t = (1- 0,41)* 4,7 t= 0,59*4,7 t ≈3 t. (7)
Treibstoff.
Um den Rückflug zur Erde antreten zu können, wäre bei einer Masse des CSM von 30 t
eine Treibstoffmenge von
MTr=[1 – 1: e(vB/ve)]*Mo= [1-1: 2,72 (0,7:2,6)]* 30 t (1- 0,76)* 30 t = 0,24*30 t ≈ 7 t (8)
zu bilanzieren.
Für die Einmündung in die Erdumlaufbahn mit einer Orbitgeschwindigkeit von 7,9 km/s aus dem Kosmos mit 11, 2 km/s beziffert sich die Treibstoffmenge bei 30 t Mo der Kommandokapsel allgemein auf
MTr=[1-1: e(vB/ve)]*Mo= [1-1: 2,72 (3,1:2,6)]*30 t=(1- 0,3)* 30 t ≈ 0,7 * 30 t = 21 t. (9)
Für den Wiedereintritt in die Erdatmosphäre muss man eine Treibstoffmasse bei einer Masse des CM von 6 t Mo
MTr= [1 – 1: e(vB/ve)]*Mo= [1-1: 2,72 (2:2,6)]* 6 t = (1- 0,46) Mo= 0,54*6 t ≈ 3 t. (10)
in Rechnung zu stellen.
5. Die Rekonstruktion des Kommandomoduls mit einer von der NASA vorgegebenen Höhe von 3,23 m und einem Durchmesser von 3,9 m, woraus im Endeffekt nur ein Gesamtvolumen von rund 12,9 m³ resultieren kann, ergab, dass nach Abzug des deklarierten Innenvolumens von 6,23 m³ das Volumen der Außenzelle der Kommandokapsel lediglich ca. 6,7 m³ hätte umfassen können. Bei einer Masse von 5,9 t hätte die Dichte der Kommandokapsel damit nur bei ca. 0,9 liegen müssen. Dies hätte nicht einmal Papier oder Pappe „leisten können“! Eine weitere mathematische Optimierung ergab dann, dass die Außenzelle nur aus einer 2,5 cm starken Aluminiumschicht hätte bestehen können – ohne Hitzeschild. Legt man die Hälfte der Gesamtmasse von 5,9 t für einen Hitzeschild zugrunde, dann hätte der Hitzschild nur aus 2 mm starkem Stahl bestehen können. Ein Kommentar dazu erübrigt sich nahezu: Das Kommandomodul wäre in der Erdatmosphäre mit einer theoretisch berechneten Bremstemperatur von mindestens 45.000 K wie eine Sternschnuppe verglüht!
6. Bereits in einer ersten Betrachtungsphase bei der Rekonstruktion der Mondlandefähre entsprechend den NASA-Parametern nach Abzug der vermeintlichen ca. MTr= 10,8 t in Rechnung gestellten Treibstoffmasse von der Startmasse mit Mo=15 t der Mondlandefähre verbleiben lediglich nur noch 4,2 t an Rüstmasse, die bereits mit der Materialrekonstruktion der Kabine (ca. 1,1 t), von Teilen der Außenzelle (ca. 1,3 t), und der deklarierten Zuladung (ca. 1,7 t), ohne Berücksichtigung des Gewichtes der Astronauten mit ihren Raumanzügen (400 kg) , der Masse für die Tanks und für die beiden Haupttriebwerke der Mondlandefähre (…) mit 600 kg weit überschritten wird. Insgesamt fehlten über 3 t Konstruktionsmasse, wie von der NASA ursprünglich angegeben und wie mit der Gesamtrekonstruktion des Lunamoduls von Apollo 11 eindrucksvoll und überzeugend belegt werden konnte.
7. Weiterhin ist das Pendelverhalten der Fahne auf dem Mond äußerst verräterisch! Denn die Pendelperiode T, die sich physikalisch mit der Pendellänge l (l=0,7 m) und der Gravitationsbeschleunigung g (g= 9,81) zu
T=2*π*√ l : g (11)
errechnet, müsste auf dem Mond
T= 6,28 *√ 0,7 m : 1,6 m/s² ≈ 4,2 s (12)
betragen. In den TV-Filmdokumentationen beträgt die Periodendauer aber nahezu 2 s, so wie eben auf der Erde. Die exakte Berechnung der Periodendauer für die Erde ergibt präzise
T= 6,28*√ 0,7 m/9,81 ≈ 1,7 s. (13)
Dieser zeitliche Unterschied von 2,5 s ist gravierend! Außerdem müsste sich auf dem Mond eine leicht gedämpfte, periodische Schwingung ergeben, da auf dem Mond keine Atmosphäre vorhanden ist. Die wahrzunehmende Schwingung ist aber fast aperiodisch. Ergo: Die Dreharbeiten erfolgten also eindeutig auf der Erde!
8. Die mechanische Instabilität der Mondlandefähre hätte eine intakte Mondlandung unmöglich gemacht! Jeder Mensch auf unseren Planeten hat bestimmt schon einmal einen missglückten Raketenstart gesehen, wenn die Rakete bereits einige Meter vom Starttisch abgehoben hat und die Triebwerke dann versagen und keine Leistung mehr erbringen. Infolgedessen bewegt sich die Rakete den physikalischen Gesetzen der Schwerkraft entsprechend wieder in Richtung der Startplattform und kippt dann aufgrund der mechanischen Instabilität einfach um, weil sich der Masseschwerpunkt gravierend verändert hat. Dies wäre auch das Schicksal der Mondlandefähre von Apollo 11 gewesen, weil kurz vor der Landung eine absolute Instabilität der Fähre bestanden hätte! Denn: Ganz grob gerechnet, hätte die aufsteigende Stufe kurz vor der Landung auf dem Mond noch ca. 5 t an Masse besessen und die absteigende Stufe hätte aufgrund des Treibstoffverbrauchs von 8 t lediglich nur noch rund 2 t an Rüstmasse gehabt. Da der Schwerpunkt der Landefähre kurz vor der Landung der Fähre auf dem Mond exakt bei 2,10 m über die Düsen gelegen haben muss, würden sich die Drehmomente wie 2,5 zu 1 bis 3: 1 verhalten haben. Damit hätte ein absolut instabiles mechanisches System vorgelegen! Jede noch so kleinste Erschütterung, wie Vibrationen durch das Triebwerk oder Druckschwankungen der ausströmenden Gase in der Düse des Triebwerkes hätten die Mondlagefähre einfach umkippen lassen! Eine Mondlandung wäre zwar „geglückt“, aber eine Rückkehr vom Mond wäre damit unmöglich gewesen. Da aber alle Akteure von Apollo 11 glücklicherweise das imaginäre Abenteuer überlebt haben, kann messerscharf geschlussfolgert werden, dass keine Mondlandung stattgefunden hat.
Die Lösung des physikalischen Problems liegt darin, dass der Schwerpunkt einer Landefähre einfach auf Höhe der Düsen des Triebwerkes liegen muss, so wie die Chinesen dies im Dezember 2013 realisieren und praktizierten. Das Problem der Senkrechtlandung von Raketen hat man erst Ende 2015/Anfang 2016 mit der Falcon 9 gelöst!
9. Ja und ca. 1 t Natriumperoxid wären für die dreiköpfige Besatzung für die Regeneration von Sauerstoff aus dem CO2 erforderlich gewesen!
10. Immer wieder wird die Behauptung strapaziert und kolportiert, dass sich auf der Mondoberfläche Laserreflektoren mit einer Flächengröße von 0,46 *0,46 m² ≈ 0,21 m² befinden würden, die die Apollo-Astronauten auf dem Mond bei ihrer Expedition dort angeblich installiert hätten, so dass mit Lasern von der Erde aus diese Reflektoren angepeilt werden könnten, womit der indirekte Beweis für die angebliche Apollomissionen geführt werden kann. Dies ist physikalischer Blödsinn!
Denn: Auch ein Laser besitzt eine gewisse Streuung, die minimal bei ca. 0,1 µm/m liegt. Dies bedeutet auf 384.401 km Erde-Mond-Entfernung (mittlere Distanz Erde -Mond) eine Streuung von rund 38,44 m (siehe auch Lindner, 1973). Wenn ein Laser-Signal, also ein Laser-Strahl die Tripel-Reflektoren treffen würde, dann könnte nur noch ein geringer Teil der ursprünglichen Energie von rund 0,21 m²: 38,44 m² ≈ 5,5*10-3 = 0,0055 vom Mond zur Erde zurück gelangen. Um sich diese Dimension konkret und bildlich zu verdeutlichen, sei folgendes dazu ausgeführt: Momentan liegt die Leistung von Hochenergielasern im kW-Bereich, wobei dann vom Mond aus nur noch eine Leistung von 5,5 Watt (zum Vergleich: eine Glühbirne hat beispielsweise 100 W Leistung) zurückgesendet werden könnte. Retour zur Erde würde der Strahl mit einer Mächtigkeit von 0,21 m² Fläche sich weiter extrem auffächern, so dass auf die Erdatmosphäre auftreffend, nur noch ein verschwindend geringes Signal mit einer ganz minimalen Leistung von 0,03 W registrierbar wäre, das von der Erdatmosphäre in jedem Falle völlig absorbiert werden würde. Im Klartext: auf der Erde würde kein Signal mehr vom ursprünglich ausgesendeten Lasersignal registrierbar oder nur noch ein natürliches Eigenrauschen des Lasers detektierbar! Übrigens: in der N 24 –TV-Sendung zu Apollo 11 am 14.11.2009 gegen 20.50 Uhr, wo dieses Laserverfahren zum Anpeilen der Tripel-Reflektoren auf dem Mond „demonstriert“ wurde, äußerte der Direktor der texanischen Sternwarte, Jerry Wiant süffisant, dass die Signale nicht vom Mond stammen, sondern vom Objektiv des Teleskops!
P.S. Übrigens hatte der Autor den skeptischen Gedanken zur Instabilität der Mondlandefähre zur Mondlandung bereits im Sommer 1969 ganz spontan für ca. 1 s gehegt gehabt!
Siegfried Marquardt, Königs Wusterhausen
Wie alle Kommentare dieses in Fachkreisen bekannten und berüchtigten Verschwörungstheoretikers wurde auch dieser Kommentar als abschreckendes Beispiel freigegeben. Die Leser, die sich intensiver mit diesen Themen beschäftigen, wissen natürlich, dass seine Ausführungen weit in Bereich der Verschwörungstheorien fallen und keinerlei wissenschaftliche Grundlage haben. Die Leser, die sich noch nicht tiefgehender mit den physikalischen Grundlagen bezüglich Mondlandung und Raketentechnik beschäftigt haben, brauchen seine Ausführungen nicht ernst nehmen – sie sind Blödsinn, salopp gesagt.
Mit der 1. und 2. Stufe der Saturn-5-Rakete konnte nicht einmal die Erdumlaufbahn erreicht werden!
In den gängigen Darstellungen der NASA soll sich das Szenario von Apollo 11 nach dem Start so abgespielt haben: Mit der ersten und zweiten Stufe gelangte Apollo 11 in die Erdumlaufbahn. Nach 10 Minuten (11 Minuten – die Angaben variieren hier) wurde die dritte Stufe gezündet und das CSM wurde auf die zweite kosmische Geschwindigkeit von 11,2 km/s beschleunigt (so wird es auch im Internet sinngemäß kolportiert). Mit der 1. und 2. Stufe der Saturn- 5-Rakete konnte Apollo 11 niemals in den Orbit gelangen! Denn: Entsprechend der Raketengrundgleichung
vB= ve * ln (Ml+ MTr): Ml = ve * ln (Mo: Ml ) (1)
konnte man mit den ersten beiden Stufen nach einer Modifikation der Formel (1) theoretisch entsprechend den Parametern der NASA (erste Stufe ve=2,6 km/s und zweite Stufe ve=4 km/s) nur eine maximale Bahn- respektive Brennschlussgeschwindigkeit von
vB=2,6 km/s*ln (2940:654) + 4,2 km/s* ln(654:164) ≈ 2,6 km/s*1,5 + 4,2*km/s 1,38 ≈
3,9 km/s+5,8 km/s = 9,7 km/s (2)
ohne Berücksichtigung der Gravitation und des Luftwiderstandes erzielt werden. Davon sind für die Reduzierung durch die Gravitation rund
∆v=t1*g+t2*g1*0,71= 161 s*9,81 m/s² + 360 s*9,5 m/s²*0,71=1580 m/s+2430 m/s ≈
4000 m/s=4 km/s (3)
zu subtrahieren (t1=Brennschlusszeit der ersten Stufe und t2 =Brennschlusszeit der zweiten Stufe; Erdbeschleunigung g= 9,81 m/s² für die erste Stufe und g1=9,5 m/s² für die zweite Stufe). Durch den Luftwiderstand müssen weitere 1 km/s kalkuliert und abgezogen werden. Damit konnte mit den ersten beiden Stufen der Saturn-5-Rakte nur eine Geschwindigkeit von 5,7 km/s erzielt werden und nicht die notwendigen 7,9 km/s. Die Astronauten konnten also gar nicht mit den beiden ersten Stufen in den Orbit gelangt sein! Mit der dritten Stufe gelangte Apollo 11 gerade einmal mit Ach und Krach in die Erdumlaufbahn, aber erzielte niemals die 2. Kosmische Geschwindigkeit! Die Astronauten von Apollo 11 bis N haben ganz lustig acht und mehr Tage lang die Erde umrundet.
Siegfried Marquardt, Königs Wusterhausen